关键词: 教师资格证

扫码添加专属备考顾问
▪ 0元领取考点真题礼包
▪ 获取1对1备考指导
全国教资备考群:737804026(点击进群,群内定期分享教资备考笔面通关资料包,并有客服老师答疑解惑)
内容:
观察:观察函数f(x)=x和f(x)=1/x的图象(图1.3-9),并完成下面的两个函数值对位表,你能发现这两个函数有什么共同特征吗?
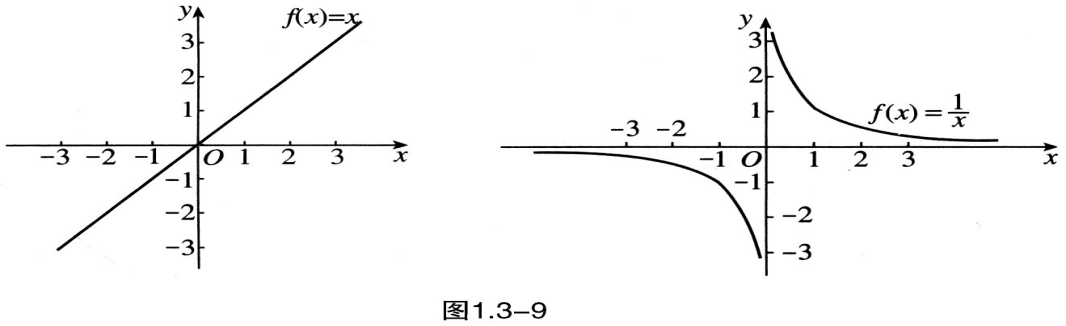
x … -3 -2 -1 0 1 2 3 … f(x)=x … 0 … x … -3 -2 -1 0 1 2 3 … f(x)= … / …![]() 1/x
1/x
我们看到,两个函数的图象都关于原点对称。函数图象的这个特征,反映在函数解析式上就是:
当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数。
例如,对于函数f(x)=x有:
f(-3)=-3=-f(3);
f(-2)=-2=-f(2);
f(-1)=-1=-f(1)。

实际上,对于函数f(x)=x定义域R内任意一个x,都有f(-x)=-x=-f(x)。这时我们称函数f(x)=x为奇函数。
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd function)。
基本要求:
(1)能利用函数图象探究出奇函数的特点;
(2)教学中注意师生间的交流互动,有适当的提问环节;
(3)请在10分钟内完成试讲内容。
答辩题目:
1. 一个函数不是奇函数就是偶函数对吗?如果不对,请举例。
2. 本节课的教学目标是什么?
试讲答案:
各位考官:大家好,我是高中数学组的XX号考生,今天我试讲的题目是《奇函数》,下面开始我的试讲。
一、导入新课
师:在初中我们学过了中心对称图形的定义,请大家回忆一下。
师:大家掌握得都很牢固。在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形。平行四边形是中心对称图形吗?
师:学生1说平行四边形是中心对称图形,绕平行四边形的中心旋转180°,旋转后的图形与原来的重合,所以它是中心对称图形。
师:那么现在给大家一个函数f(x)=x,你们能判断它的图象是不是中心对称图形吗?用代数方法呢?
师:今天我们就来学习奇函数,学过之后大家就知道怎么用代数方法判断函数的中心对称性了。
二、生成新知
师:观察函数f(x)=x和f(x)=1/x的图象,并完成下面两个函数值对应表,你能发现这两个函数有什么共同特征吗?计算并思考,5分钟后我请同学来回答。
师:学生2说通过观察和运算逐步发现两个函数具有的共同特征:图象沿原点旋转180°后与原来完全重合,也就是说这两个函数的图象都是中心对称图形。
师:这是从几何角度看出的,不错。那么从代数角度呢,你能得到一样的结论吗?试着从函数值对应表上找一找。
师:学生3说,对于函数f(x)=x,有f(-1)=-1=-f(1),f(-2)=-2=-f(2)…
师:学生4说通过函数值对应表可以看出,当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数。
师:大家观察得都很认真。那谁能用函数表达式表示一下这个结论?
师:学生5说f(-x)=-f(x)。
师:是的,一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么这个函数f(x)就叫做奇函数。
师:以这两个奇函数为例,再观察一下x的取值,你能发现奇函数的定义域有什么特征?对于任意的一个x,是否有一个-x与它对应呢?
师:对的,奇函数的定义域关于原点对称。
师:如果一个函数的图象是以坐标原点为对称中心的中心对称图形,能否判断它是不是奇函数?我们一起尝试把奇函数图象的性质总结出来。
师:奇函数图象的对称性:如果一个函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心对称图形。反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数。
三、巩固练习
师:已知y=f(x)是奇函数,且f(-6)=3,则f(6)=?
师:学生6你来回答。
师:学生6说由奇函数的性质能够得到f(6)=-f(-6)=-3。
师:试判断这几个函数是不是奇函数:①f(x)=x3+2;②f(x)=x4;③f(x)=x+1/x;④ 。做完之后小组内互相对一对答案,交流讨论一下。
。做完之后小组内互相对一对答案,交流讨论一下。
四、小结作业
师:通过这节课的学习你有什么收获?
师:好。课后将本节课练习题的1,2,5题做到练习本上。
五、板书设计
奇函数
定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
特征
定义域
图象
我的试讲到此结束,谢谢各位考官的聆听。
答辩答案:
1. 这种说法是不对的。比如函数f(x)=x2+2x+1就既不是奇函数也不是偶函数。
2. 教学目标:
知识与技能:理解奇函数的概念,知道奇函数的定义域关于原点对称,并能熟练利用定义法判断一个函数是不是奇函数。
过程与方法:通过探究奇函数的活动,培养类比、观察、归纳、思考与创新能力,体会由特殊到一般、具体到抽象的数学思维方法,并从中感受数形结合的巨大魅力。
情感态度与价值观:通过本节课的学习,激发学习信心与参与热情,培养良好的数学素养与学习习惯。
☟☟☟
添加教师资格客服老师微信
备注“网站”
获取更多考试资讯和海量备考干货


相关推荐:
手机登录确认
微信扫码下载
微信扫一扫,即可下载